Din forvirring stammer fra det faktum, at dit sind (og WX GUI scope sink) bruger lineær interpolation mellem prøverne.

Det er ikke korrekt - i dit tilfælde, hvor signalperioden ikke er et helt antal prøver, bliver dette tydeligt af det faktum, at ting ikke ser meget sinusformet ud. De er stadig (jeg lover;)).

Tænk over det sådan: ved nøjagtigt 16 kHz samplet med 32 kHz, får du 2 prøver pr. Periode, ikke? Så hvis disse prøver tilfældigvis ligger på cosinusens ekstrema, får du $ [+ 1 \, -1 \, +1 \, -1 \, \ ldots] $.

Med 13,7 kHz, ikke så langt væk fra det, får du "for det meste" også skiftende tegn, men hver så og så mange prøver, "rammer" du stadig den samme øvre eller nedre halvdel af en cosinus to gange. Derfor ser ting ud uregelmæssigt ud.

Tingene er i perfekt, flot form! Jeg har lavet en hurtig Jupyter Notebook til illustration. Hvis du ikke har tid til at læse det, er det takeaway:

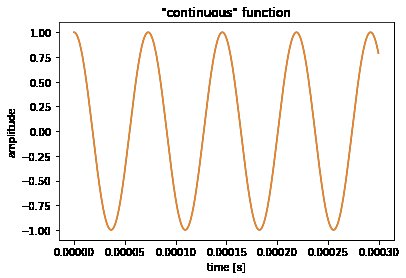
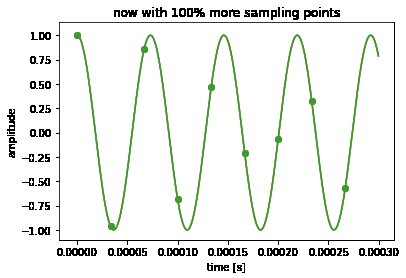
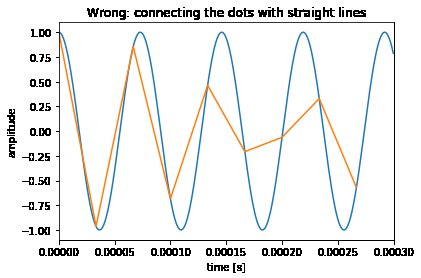
Hvad du skal gøre, mentalt, er interpolering ved hjælp af en $ \ mathrm {sinc} $ -funktion som interpolator. (Jeg gjorde det i den forbedrede version af den bærbare computer med de større billeder i sidste del.)

Hele pointen er, at selvom det måske ikke ligner det, er disse " takkede "prøver af en 13,7 kHz svingning stadig er 100% den svingning, og indeholder al den information, det kontinuerlige signal havde. Pænt!